Question

Consider f and c below. f(x, y, z) = yzexzi + exzj + xyexzk,

c.r(t) = (t2 + 4)i + (t2 − 4)j + (t2 − 5t)k, 0 ≤ t ≤ 5 (a) find a function f such that f = ∇f.

Answer 1

`f(x,y,z)=ye^(xz)+C`

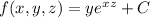
Explanation:

We can write the given expression as :

`\vec f(x,y,z)=yze^(xz)\,\vec\imath+e^(xz)\,\vec\jmath+xye^(xz)\,\vec k`

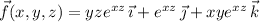
As given, f = ∇f.

∇f =
`(\partial f)/(\partial x)i` +
`(\partial f)/(\partial y)j` +
`(\partial f)/(\partial z)k`

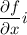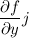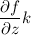
We can write the partial derivative with respect to x, y and z.

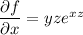`(\partial f)/(\partial x)=yze^(xz)` ___(Equation 1)

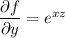`(\partial f)/(\partial y)=e^(xz)` ______(Equation 2)

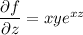`(\partial f)/(\partial z)=xye^(xz)` ______(Equation 3)

Take equation 2 and integrate with respect to y,

`(\partial f)/(\partial y)=e^(xz)`

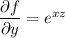
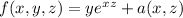`f(x,y,z)=ye^(xz)+a(x,z)` ----------Equation 4

Derivate both sides w.r.t x , we get :

`(d)/(dx)(yze^(xz))=yze^(xz)+(\partial a)/(\partial x)`

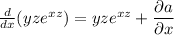
or

`(\partial a)/(\partial x)=0`

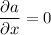
integrate

a(x,z)=b(z)

put in equation 4 ,

we get :

`f(x,y,z)=ye^(xz)+b(z)`

take derivative wrt z

`(d)/(dz) (ye^(xz)+b(z))\impliesxye^(xz)=xye^(xz)+(db)/(dz)`

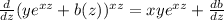
we can take here:

`(db)/(dz) = 0`

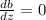
integrate:

`\int\ {(db)/(dz) } \, =\int0`

b(z) = C

The function can be written as :

from equation 4 :

`f(x,y,z)=ye^(xz)+C`

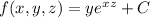
Where C is a constant.