Answer:
It's only valid when the product of m and n is zero, that is when n=0 or m=0
Explanation:
Square roots
Taking the square root of a real number m (non-negative) means to find another number x, such that
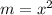
When we find square roots in algebraic expressions and we need to get rid of them, we take the 2nd power of the roots to eliminate them
We have to test if
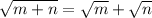
for all values of m and n
To find an answer, we take the second power in both sides:
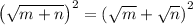
Expanding
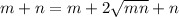
Simplifying
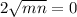
Operating
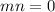
The original expression is only valid when the product of m and n is zero, that is when n=0 or m=0