Question

How many positive integers less than 100 have at least one digit that is a 9? (Let T be the set of positive integers less than 100 with a 9 in the ten's place. Let O be the set of positive integers less than 100 with a 9 in the one's place. Now determine T ∪ O).

Answer 1

19

Explanation:

Let T be the set of positive integers less than 100 with a 9 in the ten's place.

T = {90, 91, 92, 93, 94, 95, 96, 97, 98, 99}

n(T) = 10

Let O be the set of positive integers less than 100 with a 9 in the one's place.

O = {9, 19, 29, 39, 49, 59, 69, 79, 89, 99}

n(O) = 10

The common element is 99.

`T\cap O={99}`

`n(T\cap O)=1`

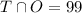
The union of both sets is

`n(T\cup O)=n(T)+n(O)+n(T\cap O)`

`n(T\cup O)=10+10-1`

`n(T\cup O)=19`

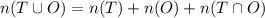
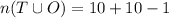
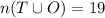
Therefore, 19 positive integers are less than 100 those have at least one 9.