Answer:
9 feet
Explanation:
Given:
The border of the garden is a right angled triangle.
Two lengths are given as 12 ft and 15 ft.
Let the length of the shortest timber be 'x' feet.
Now, in a right angled triangle, the longest length is called the hypotenuse.
As 15 feet is the largest length, it is the hypotenuse of the triangle. Now, applying Pythagoras theorem, we get:
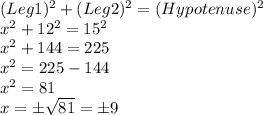
The negative value is neglected as length can never be negative.
Therefore, the length of the shortest timber is 9 feet.