Question

Two consecutive terms in a geometric sequence is giving. find the giving terms...​

Answer 1

f(5) = 20

f(6) = 40

Explanation:

The
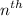`$ n^(th) $` term of a GP is given by:

`$ a_n = ar^(n - 1) $`

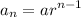
where 'a' is the first term and

'r' is the common difference.

It is given that f(3) = 5 and f(4) = 10

`$ \implies ar^2 = 5 $`

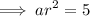
and
`$ ar^3 = 10 $`.

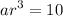Dividing them we get:

`$ (ar^3)/(ar^2) = (10)/(5) $`

`$ \implies r = 2 $`

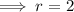
i.e, Common difference, r = 2

Now,
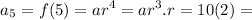`$ a_5 = f(5) = ar^4 = ar^3. r = 10(2) = $` 20

Similarly,
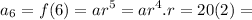`$ a_6 = f(6) = ar^5 = ar^4.r = 20(2) = $` 40

Hence, the answer.