Question

Steve can afford a $330-per-month car payment. if he is being offered a 6-year car loan with an APR of 1.2%, compounded monthly, what is the value of the most expensive car he can afford?

Answer 1

22,913.76

Explanation:

A p e x.. (:

Answer 2

$ 3934.38 ( approx )

Explanation:

Since, the monthly payment formula of a loan,

`P=(PV((r)/(12)))/(1-(1+(r)/(12))^(-n))`

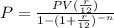
Where,

PV = present value of loan,

r = annual rate of interest,

n = number of months,

If P = $ 330, r = 1.2% = 0.012,

Number of months in 6 years, n = 12 × 6 = 72

By substituting the values,

`330 = (PV((0.012)/(12)))/(1-(1+(0.012)/(12))^(-72))`

`330 =(PV(0.001))/(1-(1.001)^(-12))`

`\implies PV = 330* (1-(1.001)^(-12))/((0.001))`

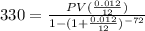
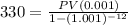
Using calculator,

PV ≈ $ 3934.38

Hence, the value of the most expensive car he can afford would be $ 3934.38 ( approx )