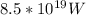Question

A fission-based nuclear bomb such as those used in World War II) uses the nuclear reactions (8.5x 10^13 J) and amount of fuel of 9.4 kg. However, by alloweing an uncontrolled chain reaction to occur, all of the bomb's energy can be released in about 1.0 x 10^-6 s. What is the average power of the nuclear bomb?

Answer 1

To solve this problem we must use the mathematical relations concerning the Power as a function of the energy released in a certain period of time. In other words:

`P = (E)/(t)`

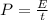
Where,

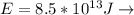`E = 8.5*10^(13)J \rightarrow` Energy

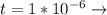`t = 1*10^(-6) \rightarrow` time

Replacing this values we have that

`P = (8.56*10^(13)J)/(1*10^(-6)s)`

`P = 8.5*10^(19)W`

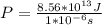
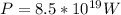
Therefore the average power of the nuclear bomb is
`8.5*10^(19)W`