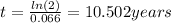Answer:
a) p(t) = P 0 e 0066t
b)
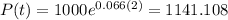
c)
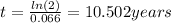
Explanation:
Part a
We have the following model:
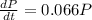
We can rewrite the expression like this:
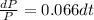
If we integrate noth sides we got:
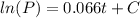
And exponentiating both sides we got this:

So the correct option would be:
a) p(t) = P 0 e 0066t
Part b
On this case we want to find the amount of money after two years if the initial investment is 1000 and the value of t=2. If we replace we got:
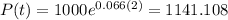
Part c
On this case we need a value of time in order to duplicate the initial amount invested, so we need to solve the following equation:
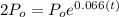
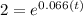
If we apply natural log on both sides we got:
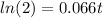
And if we solve for t we got: