Question

A projectile is thrown upward so that its distance above the ground after t seconds is h = -16t2 + 440t.

After how many seconds does it reach its maximum height?

28 s
7 s
21 s
14 s

Answer 1

14 s

Explanation:

We notice that the expression that shows the distance above ground as a function of time, is in fact a quadratic expression (parabola) with negative leading coefficient (-16). this means that the graph of the projectile's distance from the ground is a parabola with branches pointing down, and therefore must have a maximum value at its vertex.

We can then used the formula for finding the horizontal position of the vertex in a quadratic function of the general form
`y=ax^2+bx+c`:

`x_(vertex)=-(b)/(2a)`

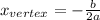
In our polynomial
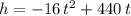`h=-16\,t^2+440\,t`, the horizontal variable is the time (t), the value of
`a` is "-16", and
`b` is "440". Therefore, the time (horizontal variable) at which the projectile reaches the maximum height is:

`t_(vertex)=-(440)/(2\,(-16)) \\t_(vertex)=(-440)/(-32) \\t_(vertex)=13.75 \,seconds`

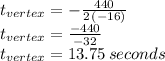
So we can round this answer to the nearest integer giving us about 14 seconds.