Question

Fidel has a rare coin worth \$550$550dollar sign, 550. Each decade, the coin's value increases by 10\%10%10, percent.

Which expression gives the coin's value, 666 decades from now?

Choose 1 answer:

Choose 1 answer:


(Choice A)

A

550\cdot 0.1^6550⋅0.1

6

550, dot, 0, point, 1, start superscript, 6, end superscript


(Choice B)

B

550(1+0.1)^6550(1+0.1)

6

550, left parenthesis, 1, plus, 0, point, 1, right parenthesis, start superscript, 6, end superscript


(Choice C)

C

550+0.1^6550+0.1

6

550, plus, 0, point, 1, start superscript, 6, end superscript


(Choice D)

D

550+(1+0.1)^6550+(1+0.1)

6

Answer 1

Answer: c

Explanation:

Answer 2

Option B -
`550(1+0.1)^6`

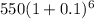
Explanation:

Given : Fidel has a rare coin worth $550. Each decade, the coin's value increases by 10%.

To find : Which expression gives the coin's value, 6 decades from now?

Solution :

The given situation represents the exponential function,

`y=a(1+r)^n`

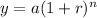
where, a is the initial value i.e. a=$550

r is the increased rate r=10%

n is the time i.e. n=6

Substitute the value in the formula,

`y=550(1+10\%)^6`

`y=550(1+0.1)^6`

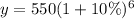
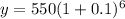
Therefore, option B is correct.