Answer:
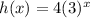 ; Vertical stretch
; Vertical stretch
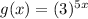 ; Horizontal compression
; Horizontal compression
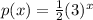 ; Vertical compression
; Vertical compression
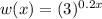 ; Horizontal stretch
; Horizontal stretch
Explanation:
The given parent function is
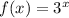
The transformation between two functions is defined as
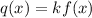
If 0<k<1, then it is vertical compression and k>1 then it is vertical stretch.
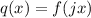
If 0<j<1, then it is horizontal stretch and j>1 then it is horizontal compression.
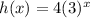
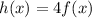
Here, k=4, therefore it is vertical stretch.
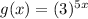
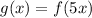
Here, j=5, therefore it is horizontal compression.
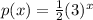
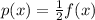
Here, k=1/2, therefore it is vertical compression.
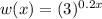
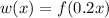
Here, j=0.2, therefore it is horizontal stretch.