Answer:
The midpoint of the midsegment of the trapezoid is (p+r+s,2q).
Explanation:
The vertices of the trapezoid are O(0,0), A(4p,4q), B(4r,4q) and C(4s,0).
If a line connects the midpoints of the two nonparallel sides of the trapezoid then it is known as midsegment of a trapezoid.
OC and AB are horizontal lines because the y-coordinated of their end points are same.It means OC and AB are parallel sides. So, we can say that OA and BC are non parallel sides.
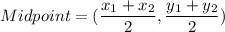
Midpoint of OA is
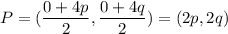
Midpoint of BC is
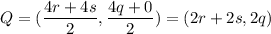
Midpoint of the midsegment of the trapezoid is the midpoint of P and Q. So, the midpoint of PQ is
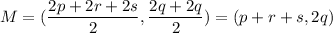
Therefore, the midpoint of the midsegment of the trapezoid is (p+r+s,2q).