Question

What is the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y = 27 − x^2? show your work.

answer choice

324

108

18

3

Answer 1

Option B.

Explanation:

The given curve is

`y=27-x^2`

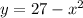
We need to find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve
`y=27-x^2`.

Let the vertex in quadrant I be (x,y), then the vertex in quadrant II is (-x,y) .

Length of the rectangle = 2x

Width of the rectangle = y

Area of a rectangle is

`Area=Length* width`

`Area=2x* y`

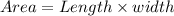
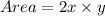
Substitute the value of y from the given equation.

`Area=2x(27-x^2)`

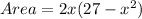
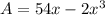`A=54x-2x^3` .... (1)

Differentiate with respect to x.

`(dA)/(dx)=54-6x^2`

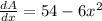
Equate
`(dA)/(dx)=0`, to find the critical points.

`0=54-6x^2`

`6x^2=54`

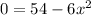
Divide both sides by 6.

`x^2=9`

`x=\pm 3`

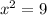
The value of x can not be negative because side length can not be negative.

Substitute x=3 in equation (1).

`A=54(3)-2(3)^3`

`A=162-54`

`A=108`

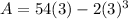
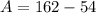
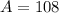
The area of the largest rectangle is 108 square units.

Therefore, the correct option is B.