Question

Find the resultant gravitational force exerted on the object at the origin by the other two objects. The universal gravitational constant is 6.672 × 10−11 N · m2 /kg2 . Answer in units of N.

Answer 1

The resultant gravitational force is
`7.76*10^(-11)\ N`

Step-by-step explanation:

Suppose A coordinate system is constructed on the surface of a pool table, and three objects are placed on the coordinate system as follows: a 1.2 kg object at the origin, a 3 kg object at (0 m,1.8 m), and a 4.6 kg object at (4 m,0 m).

We need to calculate the gravitational force along x axis

Using formula of gravitational

`F_(1)=(GmM)/(r^2)`

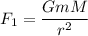
Where, m = mass of first object

M = mass of object when placed at center

r = distance

G = gravitational constant

Put the value into the formula

`F_(1)=(6.672*10^(-11)*1.2*4.6)/((4)^2)`

`F_(1)=2.301*10^(-11)\ N`

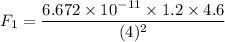
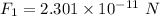
We need to calculate the gravitational force along y axis

Using formula of gravitational

`F_(2)=(Gm_(1)M)/(r^2)`

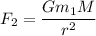
Put the value into the formula

`F_(2)=(6.672*10^(-11)*1.2*3)/((1.8)^2)`

`F_(2)=7.413*10^(-11)\ N`

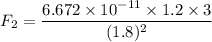
We need to calculate the resultant gravitational force

Using formula of resultant gravitational force

`F_(net)=\sqrt{(F_(1)^2+F_(2)^2)}`

`F_(net)=\sqrt{(2.301*10^(-11))^2+(7.413*10^(-11))^2}`

`F_(net)=7.76*10^(-11)\ N`

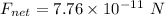
Hence, The resultant gravitational force is
`7.76*10^(-11)\ N`