Question

What is the vertex of the absolute value function defined by f(x)=|x-2|-7?

(2,7)

(-2,-7)

(-2,7)

(2,-7)

Answer 1

(2,-7)

Explanation:

Answer 2

Answer: (2,-7)

Explanation:

We know that ,

The general form of absolute value function :
`a|x-h|+k`

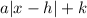
, where (h,k) is representing the vertex.

The given absolute value function:
`f(x)=|x-2|-7`

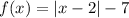
which can be written as
`f(x)=|x-2|+(-7)`

When we compare the given absolute function to its general form , then we get

h=2 , k= -7

⇒ The vertex of the function is : (2,-7)

Hence, the correct answer is (2,-7) .