Answer:
82780.42123 m/s
14.45 days
Step-by-step explanation:
m = Mass of the planet
M = Mass of the star =
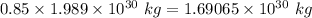
r = Radius of orbit of planet =
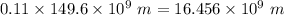
v = Orbital speed
The kinetic and potential energy balance of the planet and star system is given by
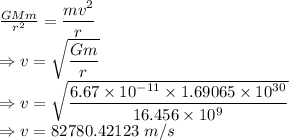
The orbital speed is 82780.42123 m/s
The orbital period is given by

Converting to days
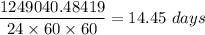
The orbital period is 14.45 days