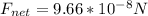Question

Three very small spheres of mass 2.50 kg, 5.00 kg, and 8.00 kg are located on a straight line in space away from everything else. The first one is at a point between the other two, 8.0 cm to the right of the second and 20.0 cm to the left of the third. Compute the net gravitational force it exerts.

Answer 1

The net gravitational force it exerts is
`F_(net)=9.66*10^(-8)N`

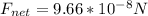
Step-by-step explanation:

Newton's Law of Gravitation can be written as

`F=(Gm_(1)m_(2))/(r^(2) )`

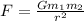
where G is the Gravitational Constant, m1 and m2 are the masses of two objects, and r is the distance between them. In this case, the spheres are loacted in straight line, so instead of a vector r, we have a distance x in meters. The distances and masses are given in the problem, and the smaller sphere is between the other two spheres. This means the sphere 1 is in the middle, the sphere 2 is on the left of 1, and the sphere 3 is on the right of 1, so

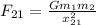`F_(21) =(Gm_(1)m_(2))/(x_(21)^(2) )` is the force that 2 feels because of 1, and

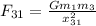`F_(31) =(Gm_(1)m_(3))/(x_(31)^(2) )` is the force that 3 feels because of 1.

If we replace the data in those previous equations, we have that

`F_(21) =(G(2.5)(5) )/((0.08)^(2) )=1.3*10^(-7)N`

`F_(31) =(G(2.5)(8) )/((0.2)^(2) )=-3.34*10^(-8)N`

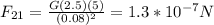
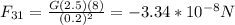
Finally, adding both results, the net force the sphere 1 exerts is

`F_(net)=9.66*10^(-8)N`