Answer:
The velocity of the police car is, v = 17.798 m/s
Step-by-step explanation:
Given data,
The actual frequency of the siren, f = 2010 Hz
The observed frequency of siren is, f' = 2120 Hz
The velocity of the observer, v' = 0 m/s
The velocity of the source, v = ?
The formula for Doppler effect,
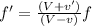
Where,
V - velocity of sound waves in air.
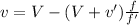
Substituting the given values,
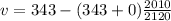
v = 17.798 m/s
Hence, the velocity of the police car is, v = 17.798 m/s