Answer:
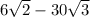
Explanation:
Remember that:
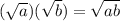
![\sqrt[n]{a^n}=a](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7n3agtxpmdkpp0ixo9p04d3znbyw20xqj1.png)
Given the following expression:
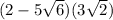
The steps to simplify this expression, are:
1. Apply the Distributive property:
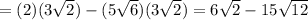
2.Since:

You can rewrite the radicand 12 in this form:
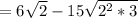
3. Simplifying, you get:
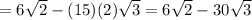
4. Notice that the indices of the Radicals are the same, but the radicands don't, then, you can subtract the Radicals.