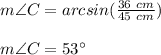Question

What is m∠C?

Round the value to the nearest degree.

Answer 1

Answer:
`m\angle C=53\°`

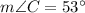
Explanation:

For this exercise you need to use the Inverse Trigonometric function arcsine, which is defined as the inverse function of the sine.

Then, to find an angle α, this is:

`\alpha =arcsin((opposite)/(hypotenuse))`

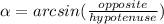
In this case, you can identify that:

`\alpha =m\angle C\\\\opposite=AB=36\ cm\\\\hypotenuse=AC=45\ cm`

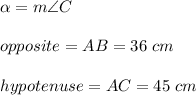
Then, substituting values into
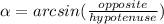`\alpha =arcsin((opposite)/(hypotenuse))` and evaluating, you get that the measure of the angle "C" to the nearest degree, is:

`m\angle C=arcsin((36\ cm)/(45\ cm))\\\\m\angle C=53\°`