Answer:
OPTION B: f(n) = 4 +3n
Explanation:
Substitute n =1 in each of the options. We compare the given sequence and the result obtained.
OPTION A: f(n) = 4(3)

Substituting n =1, we get: f(1) =
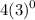 = 4.
= 4.
But, in the given sequence the first term is 7. So, this is not the recursive form.
OPTION B: f(n) = 4 + 3n
Substituting n = 1 2, 3, 4, 5
f(1) = 4 + 3(1) = 7
f(2) = 4 + 3(2) = 10
f(3) = 4 + 3(3) = 13
f(4) = 4 + 3(4) = 16
f(5) = 4 + 3(5) = 19
This is exactly the sequence given.
So, we say OPTION B is the answer.
OPTION C: f(n) = 3n + 7
Substituting n = 1.
f(1) = 3(1) + 7 = 10
It is discarded.
OPTION D: f(n) =
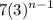
Substituting n = 1.
f(1) =
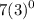 = 7
= 7
Substituting n = 2
f(2) =
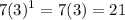
This option can be discarded as well.