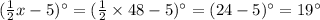Answer:
m∠EFG =
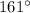
m∠LMN =
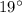
Explanation:
Given:
∠EFG and ∠LMN are supplementary angles
m∠EFG =
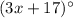
m∠LMN =
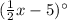
We need to find m∠EFG and m∠LMN
Now we know that sum of the Supplementary angles are 180°
Hence we can say that;
m∠EFG + m∠LMN = 180°
Substituting the given values we get;
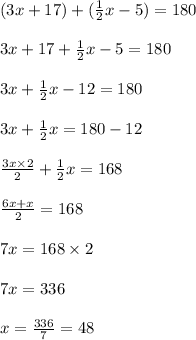
Now Substituting the value of x to find the measures of angle;
m∠EFG =

m∠LMN =