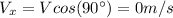Answers:
a) 12.54 m
b) 1.6 s
c) 0 m/s
Step-by-step explanation:
This problem can be solved with the following equations:
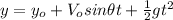 (1)
(1)
 (2)
(2)
Where:
 is the phone's final height
is the phone's final height
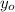 is the phone's intial height and the cliff's height
is the phone's intial height and the cliff's height
 is the initial velocite, since the phone was dropped
is the initial velocite, since the phone was dropped
 is the time it took to the phone to hit the water
is the time it took to the phone to hit the water
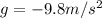 is the acceleration due gravity, always directed downwards
is the acceleration due gravity, always directed downwards
 is the angle with the horizontal
is the angle with the horizontal
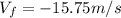 is the phone's final velocity, directed downwards
is the phone's final velocity, directed downwards
a) Let's begin by rewriting (1) and (2) acording to the information given above:
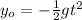 (3)
(3)
 (4)
(4)
Isolating
 from (4) and substituting in (3):
from (4) and substituting in (3):
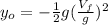 (5)
(5)
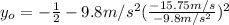 (6)
(6)
 (7) This is the height of the cliff
(7) This is the height of the cliff
b) Finding
 from (4):
from (4):
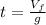 (8)
(8)
 (9)
(9)
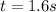 (10)
(10)
c) Since
 the horizontal velocity is:
the horizontal velocity is: