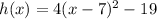Question

If g(x) = 4x^2 - 16 were shifted 7 units to the right and 3 down, what would the

new equation be?​

Answer 1

The new equation is
`h(x)=4(x-7)^2-19`

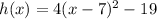
Explanation:

Given : Function
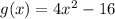`g(x) = 4x^2 - 16` were shifted 7 units to the right and 3 down.

To find : What would the new equation be?​

Solution :

Shifting to the right with 'a' unit is

f(x)→f(x-a)

So, shifting g(x) 7 units to the right is

`h(x) = 4(x-7)^2-16`

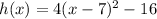
Shifting to the down with 'b' unit is

f(x)→f(x)-b

So, shifting g(x) 3 units down is

`h(x)=(4(x-7)^2-16)-3`

`h(x)=4(x-7)^2-19`

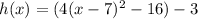
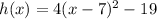
The new equation is
`h(x)=4(x-7)^2-19`