Question

A manufacturer knows that their items have a normally distributed lifespan, with a mean of 7.4 years, and standard deviation of 2.3 years. If you randomly purchase one item, what is the probability it will last longer than 4 years?

Answer 1

Answer: 0.9306

Explanation:

Given : A manufacturer knows that their items have a normally distributed lifespan, with a mean of 7.4 years, and standard deviation of 2.3 years.

i.e.
`\mu=7.4\ \ \&\ \sigma=2.3`

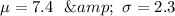
Let x denotes the lifespan of the items.

Then, the probability it will last longer than 4 years will be :-

`P(x>4)=1-P(x\leq4)\\\\=1-P((x-\mu)/(\sigma)<(4-7.4)/(2.3))\\\\=1-P(z<-1.48)\ \ [\because\ z=(x-\mu)/(\sigma)]\\\\=1-(1-P(z<1.48))\ \ [\because\ P(Z<-z)=1-P(Z<z)]\\\\=P(z<1.48)= 0.9306\ \ [\text{By z-table}]`

Hence , our required probability = 0.9306