Question

A local board of education conducted a survey of residents in the community concerning a property tax levy on the coming local ballot. They randomly selected 850 residents in the community and contacted them by telephone. Of the 850 residents surveyed, 410 supported the property tax levy. Let p represent the proportion of residents in the community that support the property tax levy. What is the 90% confidence interval for p

A. 0.4489 to 0.5159.
B. 0.4542 to 0.5105.
C. 0.4487 to 0.5161.
D. 0.4463 to 0.5185.

Answer 1

Answer: B. 0.4542 to 0.5105.

Explanation:

The confidence interval for population proportion is given by :-

`\hat{p}\pm z^* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

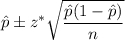
, where
`\hat{p}` = Sample proportion.

n= sample size.

z* = Critical value.

Let p represent the proportion of residents in the community that support the property tax levy.

As per given , we have

Of the 850 residents surveyed, 410 supported the property tax levy.

i.e. n= 850 ,
`\hat{p}=(410)/(850)=0.48235`

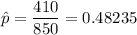
From z-table , the critical value corresponds to 90% confidence level = z*=1.645

Now, 90% confidence interval for p:

`=0.48235\pm (1.645)\sqrt{(0.48235(1-0.48235))/(850)}`

`=0.48235\pm (1.645)√(0.00029375115)`

`=0.48235\pm (1.645)(0.017139170049)`

`=0.48235\pm 0.0281939`

`=(0.48235-0.0281939,\ 0.48235+ 0.0281939)\\\\=(0.4541561,\ 0.5105439)\\\\\approx(0.4542,\ 0.5105)`

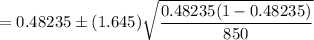
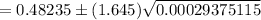
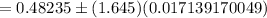
Hence, the correct answer is B. 0.4542 to 0.5105.