Answer:
The BEST statement describes how the triangle could be altered in order to make it a right triangle
B.
One inch could be removed from the 9 in. leg and a new hypotenuse could be drawn.
Explanation:
Triangle ABC has the side lengths 6 in., 9 in., and 11 in.
The only condition is that satisfy to become Δ ABC a Right angle triangle is
Longer leg (one inch remove) = 9 - 1 = 8 inch
New hypotenuse = 10 inch
So that Pythagoras theorem must satisfy
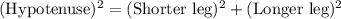
So (Hypotenuse)² = 10² = 100
(Shorter leg)² = 6² = 36
(Longer leg)² = 8² = 64
So we have,
(Shorter leg)² + (Longer leg)² = 36 + 64
= 100
= (Hypotenuse)²
Therefore, Δ ABC is right Triangle By Converse of Pythagoras Theorem.
Therefore,
The BEST statement describes how the triangle could be altered in order to make it a right triangle
B.
One inch could be removed from the 9 in. leg and a new hypotenuse could be drawn.