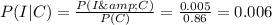Question

In a jury trial, suppose the probability the defendant is convicted, given guilt, is 0.95, and the probability the defendant is acquitted, given innocence, is 0.95. suppose that 90% of all defendants truly are guilty. find the probability the defendant was actually innocent given the defendant is convicted.

Answer 1

The probability of the defendant is innocent given the defendant is convicted is P=0.006.

Explanation:

Being:

G: guilty, I:innocent, C: convicted, A: acquitted.

We need to calculate P(I|C).

Being innocent, given convicted, is equal to the probability of being innocent and convicted divided by the probability of being convicted (innocent or guilty)

`P(I|C)=(P(I\&C))/(P(C))`

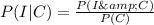
The probability of being innocent and convicted is

`P(I\&C)=P(C|I)*P(I)=0.05*0.1=0.005`

The probability of being convicted is equal to the sum of P(I&C) and P(G&C)

`P(C)=P(I\&C)+P(I\&C)=P(C|I)*P(I)+P(C|G)*P(G)\\\\P(C)=0.005+0.95*0.90=0.005+0.855=0.86`

Then,

`P(I|C)=(P(I\&C))/(P(C))=(0.005)/(0.86)= 0.006`