Question

The production department has installed a new spray machine to paint automobile doors. As is common with most spray guns, unsightly blemishes often appear because of improper mixture or other problems. A worker counted the number of blemishes on each door. Most doors had no blemishes; a few had one; a very few had two; and so on. The average number was 0.5 per door. The distribution of blemishes followed the Poisson distribution. Out of 10,000 doors painted, about how many would have no blemishes?

A. about 6,065B. about 3,935C. about 5,000D. about 500

Answer 1

10000*0.6065=6065

A. about 6,065

Explanation:

Definitions and concepts

The Poisson process is useful when we want to analyze the probability of ocurrence of an event in a time specified. The probability distribution for a random variable X following the Poisson distribution is given by:

`P(X=x) =\lambda^x (e^(-\lambda))/(x!)`

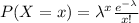
And the parameter
`\lambda` represent the average ocurrence rate per unit of time.

For this distribution the expected value is the same parameter
`\lambda`

`E(X)=\mu =\lambda=0.5` ,
`Var(X)=\lambda=0.5`,
`Sd(X)=707`

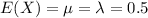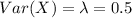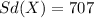
Solution to the problem

We want "how many would have no blemishes" so first we need to find the probability that X=0, since X represent on this case the number of blemishes on each door. And if we use the mass function we got this:

`P(X=0) =0.5^0 (e^(-0.5))/(0!)=0.6065`

And now since we have a total of 10000 doors painted we can find how many we would expect with no blemishes:

10000*0.6065=6065

A. about 6,065