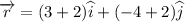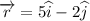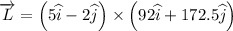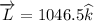Answer:
(a)
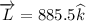
(b)
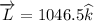
Step-by-step explanation:
mass, m = 2.3 kg
vx = 40 m/s
vy = 75 m/s
(a) Angular momentum is given by

Where, p is the linear momentum and r is the position vector about which the angular momentum is calculated.
Here,
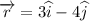
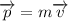
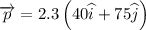
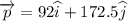
So, the angular momentum
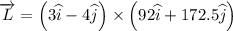
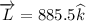
(b) Here,