Answer:
a) {x+y=405 y=8x
Explanation:
Notation
X= represents the number of angelfish Carlos bought
Y= represents the number of parrotfish he bought.
Total of fish =405
He bought 8 times as many parrotfish as angelfish
Solution to the problem
The correct system of equations are:
a) {x+y=405 y=8x
Since the addition of x+y=405 , since 405 represent the total os fishes. And the claim that "He bought 8 times as many parrotfish as angelfish" is expressed on the equation y=8x.
Now we can solve the equation, we can use for example the substitution method, let's name the equations like this:
x+y=405 (1)
y=8x (2)
If we solve x from equation (1) we got:
x=405-y (3)
And if we replace equation (3) into equation (2) we got:
y=8(405-y)=3240-8y[/tex]
And now we can solve for y like this:
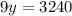 , so then y =360
, so then y =360
And replacing into equation (3) we got the value of x

And we can check that we satisfy the two conditions:
x+y=360+45=405
y=8(45)=360