Question

Let sin(−θ)=−3/5 and tanθ>0. What is the value of cos(−θ)?

A 3/5



B−3/5





C 4/5





D −4/5

Answer 1

The value of Cos (-Ф)
`(\textrm 4)/(\textrm 5)` .

Explanation:

Given Trigonometric function as :

sin( - Ф ) =
`(- 3)/(5)`

- sin Ф =
`(- 3)/(5)`

So, sin Ф =
`( 3)/(5)`

Now, as sin Ф =
`(\textrm perpendicular)/(\textrm hypotenuse)`

So ,
`(\textrm perpendicular)/(\textrm hypotenuse)` =
`( 3)/(5)`

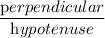
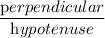So, perpendicular = 3

And hypotenuse = 5

Now, From Pythagoras Theorem

Base ² = Hypotenuse² - Perpendicular²

Or, Base ² = 5² - 3²

Or, Base ² = 25 - 9

Or, Base ² = 16

∴ Base =
`√(16)`

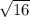
I.e Base = 4

Now, Cos Ф =
`(\textrm base)/(\textrm hypotenuse)`

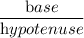
So, Cos Ф =
`(\textrm 4)/(\textrm 5)`

Now , Since

Cos ( - Ф ) = Cos Ф

So, Cos ( - Ф ) = Cos Ф =
`(\textrm 4)/(\textrm 5)`

Hence The value of Cos (-Ф)
`(\textrm 4)/(\textrm 5)` . Answer