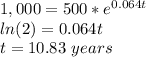Question

Suppose that Upper P0 is invested in a savings account in which interest is compounded continuously at 6.4% per year. That​ is, the balance P grows at the rate given by the following equation.

dP/dt = 0.064 P(t) ​
(a) Find the function​ P(t) that satisfies the equation. Write it in terms of P0 and 0.064.
​(b) Suppose that ​$500500 is invested. What is the balance after 22 ​years? ​
(c) When will an investment of ​$500 double​ itself?

Answer 1

(a)
`P(t) = P0*e^(0.064t)`

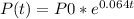
(b) P(22) = $2,043.88

(c) t=10.83 years

Explanation:

The rate of change in the balance per year is given by:

`(dp)/(dt)=0.064P(t)`

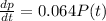
(a) Integrating this expression yields the function P(t) for the accumulated balance:

`\int(dp)/(dt) \, dt =\int(0.064P(t)) dt\\P(t) = C*e^(0.064t)`

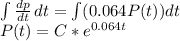
Where C is the initial invested amount P0:

`P(t) = P0*e^(0.064t)`

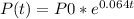
(b) For P0 = $500 ad t =22 years

`P(22) = 500*e^(0.064*22)\\P(22) = \$2,043.88`

(c) t for P(t) = $1,000 and P0 = $500

`1,000 = 500*e^(0.064t)\\ln(2) = 0.064t\\t=10.83\ years`