Height of tower to nearest meter is 111.92 meter
Solution:
Given that pole that is 3.3m tall casts a shadow that is 1.29m long
Also that at the same time, a nearby tower casts a shadow that is 43.75m long
To find: Height of tower
We can solve this by setting up a ratio comparing the height of the pole to the height of the tower and shadow of the pole to the shadow of the tower
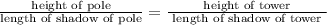
height of pole = 3.3 m
length of shadow of pole = 1.29 m
height of tower = ?
length of shadow of tower = 43.75 m
Set up a proportion comparing the height of each object to the length of the shadow,
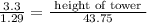
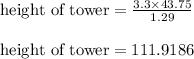
Thus the height of tower to nearest meter is 111.92 meter