Question

You throw a ball straight up with an initial velocity of 14.3 m/s. On the way up it passes a tree branch at a height of 7.8 m. How much additional time will pass before the ball passes the tree branch on the way back down? Numeric: A numeric value is expected and not an expression. t = ______________________.

Answer 1

1.47 s

Step-by-step explanation:

The equations of uniformly accelerated rectilinear motion of upward (vertical ) are:

y = y₀+ (v₀)*t - (1/2)*g*t² Equation (1)

vf² = v₀² -2gy₁ Equation (2)

vf = v₀ -gt Equation (3)

Where:

y: vertical position in meters (m)

y₀ : initial vertical position in meters (m)

t : time in seconds (s)

v₀: initial vertical velocity in m/s

vf: final vertical velocity in m/s

g: acceleration due to gravity in m/s²

Data

v₀ = 14.3 m/s

y₀ =0

y₁ = 7.8

g = 9.8 m/s²

Calculation of the time it takes for the ball to hit the ground (t)

when the ball hits the ground y = 0

We replace data in the formula (1)

y = y₀ + (v₀)*t - (1/2)*g*t²

0 = 0 + (14.3)*t - (1/2)* (9.8) *t²

4.9t²= (14.3)*t

We divided both sides of the equation by t

4.9t= (14.3)

t = (14.3)/ 4.9

t = 2.92 s

Calculation of the time it takes for the ball to reach the tree branch (t₁)

We replace data in the formula (2)

vf² = v₀² -2gy₁

vf² = (14.3)² -2(9.8)(7.8 )

vf² =204.49 -152.88

vf² = 51.61

`V_(f) = √(51.61)`

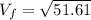
vf = 7.18 m/s

We replace data in the formula (3)

vf = v₀ -gt₁

7.18 = 14.3 -(9.8)t₁

(9.8)t₁ = 14.3 - 7.18

(9.8)t₁ = 7.116

t₁ = 7.116 / (9.8)

t₁ = 0.72 s

Additional time that will pass before the ball passes the tree branch on the way back (t₂)

t₂ = t - 2*t₁

t₂ = 2.92 s - 2*(0.72)s

t₂ = 2.92 s - 2*(0.72)s

t₂ = 1.47 s