Question

g A wheel of diameter 8.0 cm has a cord of length 6.0 m wound around its periphery. Starting from rest, the wheel is given a constant angular acceleration of 3.0 rad/s2. How long will it take the cord to unwind?

Answer 1

t = 10 s

Step-by-step explanation:

Data

D = 8.0 cm = 0.08 m : diameter of the wheel

R = D/2 = (0.08)/2 = 0.04 m : Radio of the wheel

Lc = 6.0 m : length of the cord

ω₀ = 0

α = 3.0 rad/s²

Problem development

Lw : Length of the circunference of the wheel

Lw = 2πR = 2π(0.04) m = 0.2513 m = 1 revolution

θ : angular displacement

1 revolution = 0.2513 m , Lc = 6.0 m

θ = 6.0 m * (1 rev/0.2513 m) = 23.87 rev = 23.87*2π= 150 rad

Kinematics of the wheel

θ = ω₀*t + (1/2)(α)(t)²

150 = 0 + (1/2)(3)(t)²

300 = (3) (t)²

(t)² = 100

`t = √(100)`

t = 10 s

Answer 2

To solve this problem it is necessary to apply the equations related to the description of the tangential and angular movement.

The displacement where the speed and acceleration is related is given by the equation:

`x = v_0t+(1)/(2)at^2`

Where

`v_0 =` Initial velocity (0 because start from rest)

t = time

a = Acceleration

We have angular acceleration but not tangential acceleration. Tangential acceleration can be obtained through the relationship

`a = r\alpha \rightarrow r = (diameter)/(2)`

`a = (0.08)/(2)(3)`

`a = 0.12m/s^2`

And we have also that the displacement is

`x = 6m`

Now replacing,

`x = v_0t+(1)/(2)at^2`

`6 = 0*t+(1)/(2)(0.12)t^2`

`6 = (1)/(2)(0.12)t^2`

`t = 10s`

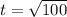
Therefore will take the cord to unwind around 10s