Question

g In 1956, Frank Lloyd Wright proposed the construction of a mile-high building in Chicago. Suppose the building had been constructed. Ignoring Earth's rotation, find the change in your weight if you were to ride an elevator from the street level, where you weigh 770 N, to the top of the building.

Answer 1

To solve this problem it is necessary to apply the concepts related to acceleration due to gravity, as well as Newton's second law that describes the weight based on its mass and the acceleration of the celestial body on which it depends.

In other words the acceleration can be described as

`a = (GM)/(r^2)`

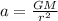
Where

G = Gravitational Universal Constant

M = Mass of Earth

r = Radius of Earth

This equation can be differentiated with respect to the radius of change, that is

`(da)/(dr) = -2(GM)/(r^3)`

`da = -2(GM)/(r^3)dr`

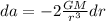
At the same time since Newton's second law we know that:

`F_w = ma`

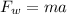
Where,

m = mass

a =Acceleration

From the previous value given for acceleration we have to

`F_W = m ((GM)/(r^2) ) = 600N`

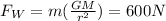
Finally to find the change in weight it is necessary to differentiate the Force with respect to the acceleration, then:

`dF_W = mda`

`dF_W = m(-2(GM)/(r^3)dr)`

`dF_W = -2(m(GM)/(r^2))((dr)/(r))`

`dF_W = -2F_W((dr)/(r))`

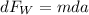
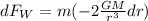
But we know that the total weight (F_W) is equivalent to 600N, and that the change during each mile in kilometers is 1.6km or 1600m therefore:

`dF_W = -2(600)((1.6*10^3)/(6.37*10^6))`

`dF_W = -0.3N`

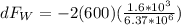
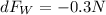
Therefore there is a weight loss of 0.3N every kilometer.