Answer:
We can conclude that the rate of undercutting is less than 5% and the goal has been met.
Explanation:
We have a goal of a rate of 5% or lower of defects. We took a sample and now we have to perform an hypothesis test of the proportions to conclude (or not) that the rate of defects is below 5%.
The null and alternative hypothesis are:
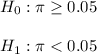
The significance level is defined as 0.05.
The sample proportion is
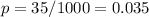
The standard deviation is
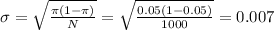
We can calculate the statistic z-value as
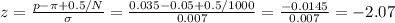
The p-value for this test statistic is

The P-value (0.02) is smaller than the significance level (0.05), so the effect is significant. There is enugh evidence to reject the null hypothesis.
We can conclude that the rate of undercutting is less than 5% and the goal has been met.