Question

Is the function ƒ(x) = e–11x an exponential function? If so, identify the base. If not, why not?

Answer 1

Yes

`y=e^(-11x)=(1)/(e^(11x))=(1)/(e^(11)) (1)/(e^x)=(1)/(e^(11)) e^(-x)`

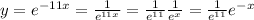
So then we see that the base on this case is:
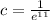`c=(1)/(e^(11))` , so then our function can be considered as an exponential function.

Explanation:

First we need to define an exponential function.

The exponential function with a base c is givn by the following expression:

`f(x)=c^x`, and
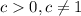`c>0, c\\eq 1` and x can be any real number.

The exponential function have always a base and a variable. The value c it's called the base and x the variable.

The exponential function is defined as:

`y=e^x`

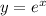
And the function given by:

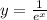`y=(1)/(e^x)` is called the natural exponential function.

For our special case our function is given by:

`y=e^(-11x)=(1)/(e^(11x))=(1)/(e^(11)) (1)/(e^x)=(1)/(e^(11)) e^(-x)`

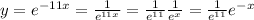
So then we see that the base on this case is:
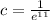`c=(1)/(e^(11))` , so then our function can be considered as an exponential function.