Question

g A projectile is shot directly away from Earth's surface. Neglect the rotation of the Earth. What multiple of Earth's radius RE gives the radial distance (from the Earth's center) the projectile reaches if (a) its initial speed is 0.216 of the escape speed from Earth and (b) its initial kinetic energy is 0.216 of the kinetic energy required to escape Earth? (Give your answers as unitless numbers.) (c) What is the least initial mechanical energy required at launch if the projectile is to escape Earth?

Answer 1

a)
`r_(max)` = 1,049
`R_(e)`

, b)
`r_(max)` = 1,276
`R_(e)`

Step-by-step explanation:

For this exercise we must look for the Earth's escape velocity, for this we use the conservation of energy at two points on the surface and one point at a very distant point.

Initial. Earth's surface

Em₀ = K + U = ½ m v² - G m M /
`R_(e)`

Final. Very far point

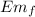`Em_(f)` = U = - G m M /
`r_(max)`

Energy is conserved

Emo =
`Em_(f)`

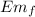
½ m v² - G m M /
`R_(e)` = - G m M /
`r_(max)`

v² = 2 G M (1 /
`R_(e)` - 1 /
`r_(max)`)

The escape velocity is defined as the speed to take the projectile to an infinite distance (
`r_(max)` = ∞)

v = √ (2GM /
`R_(e)`)

In our case the speed is v = 0.216 vesc

Let's clear the maximum height

1 /
`R_(e)` - 1 /
`r_(max)` = v² / 2GM

1 /
`r_(max)` = 1 /
`R_(e)` - v² / 2GM

We substitute and calculate

1 /
`r_(max)` = 1 /
`R_(e)` - 0.216² (2GM / Re) / 2GM

1 /
`r_(max)` = 1 /
`R_(e)` - 0.046656 /
`R_(e)`

1 /
`r_(max)` = 1 /
`R_(e)` (1 -0.046656)

`r_(max)` =
`R_(e)` / 0.953344 = 1.049
`R_(e)`

`r_(max)` = 1,049
`R_(e)`

b) the kinetic energy is 0.216 of the kinetic energy to escape from the earth

Kinetic energy

K = ½ m vesc²

K = ½ m 2GM /
`R_(e)` = A

Where A is the value of the kinetic energy of escape, in our case we have

0.216 A = ½ m v²

v² = (0.216 A) 2 / m

We substitute in the equation of maximum height

1 /
`r_(max)` = 1 /
`R_(e)` - v² / 2GM

1 /
`r_(max)` = 1 /
`R_(e)` - (0.216 A 2/m) / 2GM

We substitute the value of A

1 /
`r_(max)` = 1 /
`R_(e)` - 0.216 2/m (1/2 m 2GM /
`R_(e)`) 1 / 2GM

1 /
`r_(max)` = 1 /
`R_(e)` - 0.216 1 /
`R_(e)`

1 /
`r_(max)` = 1 /
`R_(e)` (1-0.216)

`r_(max)` =
`R_(e)` /0.784

`r_(max)` = 1,276
`R_(e)`

c) the initial mechanical energy

The definition of the escape velocity is the speed to take the body to an infinite distance with zero speed, the energy difference is zero

K = U

Em = 0