Question

Write an equation of a circle with center {-1,2} passing through the point {2,4}

Answer 1

The equation of circle passing through points (2, 4) and center (-1 , 2) is (x + 1 )² + (y - 2)² = 13

Explanation:

Given as :

The circle having center = (-1 , 2)

The circle passes through point = (2, 4)

Now, Standard equation of circle with center and passing through points is

(x - h)² + (y -k)² = r²

where h and k are the center of circle and r is the radius of circle

Now the center as (h,k) = (-1 , 2)

And passing through points (x,y) = (2, 4)

Now, satisfying the center and points on standard circle equation

I.e (x - h)² + (y -k)² = r²

Or, (2 - (-1) )²+ (4 -2)² = r²

or, 3² + 2² = r²

or, r² = 9 + 4

Or , r² = 13

∴ r =
`√(13)`

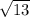
Now circle equation

(x - (-1) )² + (y -2)² = (
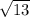`√(13)`)²

or, (x + 1 )² + (y - 2)² = 13

So, equation of circle is (x + 1 )² + (y - 2)² = 13

Hence The equation of circle passing through points (2, 4) and center (-1 , 2) is (x + 1 )² + (y - 2)² = 13 Answer

Answer 2

The equation of the circle is given by,

`(x-2)^(2) + (y-4)^(2) = (√(13))^(2)`

Explanation:

The center of the circle is given as (-1,2) and it passes through (2,4).

The distance between the two points is radius of the circle.

`(Distance) = \sqrt{(x2-x1)^(2)+(y2-y1)^(2)}`

Radius =
`\sqrt{(2-(-1))^(2)+(4-2)^(2)}`

Radius =
`√(13)`

The equation of the circle is given by,

`(x-x1)^(2) + (y-y1)^(2) = (Radius)^(2)`

Inserting above values,

`(x-2)^(2) + (y-4)^(2) = (√(13))^(2)`