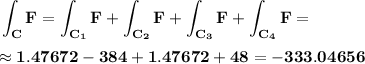Question

Let F= 6(x+y)i + 6 sin(y)j,. Find the line integral of F around the perimeter of the rectangle with corners (5,0),(5,7),(-3,7),(-3,0) traversed in that order.

line integral =_________.

Answer 1

-333.04656

Explanation:

F can be rewritten as

`\bf F(x,y)=(6(x+y),6sin(y))`

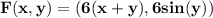
The path C on which we are going to evaluate the integral is

`\bf (5,0)\overset{C_1}{\rightarrow}(5,7)\overset{C_2}{\rightarrow}(-3,7)\overset{C_3}{\rightarrow}(-3,0)\overset{C_4}{\rightarrow}(5,0)`

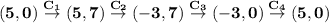
All the paths can be parametrized with parameter t (0≤ t≤ 1)

Parametrization of
`\bf C_1`

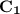
r(t) = (5,0)+t((5,7)-(5,0)) = (5,0)+t(0,7) = (5,7t)

`\bf \displaystyle\int_(C_1)F=\displaystyle\int_(0)^(1)F(r(t))\bullet r'(t)dt=\displaystyle\int_(0)^(1)(6(5+7t ),6sin(7t))\bullet (0,7)dt=\\\\42\displaystyle\int_(0)^(1)sin(7t)dt\approx1.47672`

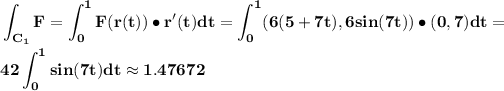
Parametrization of
`\bf C_2`

r(t) = (5,7)+t((-3,7)-(5,7)) = (5,7)+t(-8,0) = (5-8t,7)

`\bf \displaystyle\int_(C_2)F=\displaystyle\int_(0)^(1)F(r(t))\bullet r'(t)dt=\displaystyle\int_(0)^(1)(6(12-8t),6sin(7))\bullet (-8,0)dt=\\\\-48\displaystyle\int_(0)^(1)(12-8t)dt=-384`

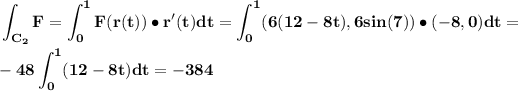
Parametrization of
`\bf C_3`

r(t) = (-3,7)+t((-3,0)-(-3,7)) = (-3,7)+t(0,-7) = (-3,7-7t)

`\bf \displaystyle\int_(C_3)F=\displaystyle\int_(0)^(1)F(r(t))\bullet r'(t)dt=\displaystyle\int_(0)^(1)(6(4-7t),6sin(-7t))\bullet (0,-7)dt=\\\\-42\displaystyle\int_(0)^(1)sin(-7t)dt\approx1.47672`

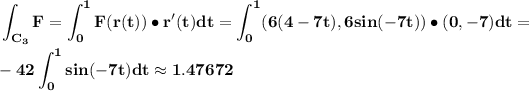
Parametrization of
`\bf C_4`

r(t) = (-3,0)+t((5,0)-(-3,0)) = (-3,0)+t(8,0) = (-3+8t,0)

`\bf \displaystyle\int_(C_4)F=\displaystyle\int_(0)^(1)F(r(t))\bullet r'(t)dt=\displaystyle\int_(0)^(1)(6(-3+8t),6sin(0))\bullet (8,0)dt=\\\\48\displaystyle\int_(0)^(1)(-3+8t)dt=48`

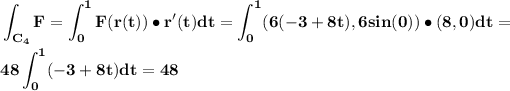
Finally

`\bf \displaystyle\int_(C)F=\displaystyle\int_(C_1)F+\displaystyle\int_(C_2)F+\displaystyle\int_(C_3)F+\displaystyle\int_(C_4)F=\\\\\approx 1.47672-384+1.47672+48=-333.04656`