Answer:
Second statement is true.
The lengths 7, 40 and 41 can not be sides of a right triangle. The lengths 12, 16, and 20 can be sides of a right triangle.
Explanation:
for first part of statement
The lengths 7, 40 and 41 can not be sides of a right triangle.
If the square of long side is equal to the sum of square of other two sides
then the given length can be sides of a right triangle.
Check the given length by Pythagoras Theorem.
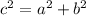 ----------(1)
----------(1)
Let
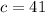 and
and
 and
and
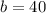
Put all the value in equation 1.
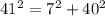
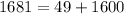
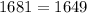
Therefore, the square of long side is not equal to the sum of square of other two sides, So given lengths 7, 40 and 41 can not be sides of a right triangle.
for second part of statement.
The lengths 12, 16, and 20 can be sides of a right triangle.
Check the given length by Pythagoras Theorem.
Let
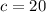 and
and
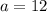 and
and
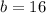
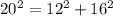
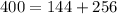
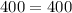
Therefore, the square of long side is equal to the sum of square of other two sides, So given the lengths 12, 16, and 20 can be sides of a right triangle.
Therefore, The lengths 7, 40 and 41 can not be sides of a right triangle. The lengths 12, 16, and 20 can be sides of a right triangle.