Question

Solve x2 + 14x = −24 by completing the square.

What is the solution set of the equation?

{−12, −2}
{−7, 7}
{−6, −4}
{−5, 5}

Answer 1

A. -12, -2

Explanation:

Just took an Edge quiz.

Answer 2

Option A

The solution set of the equation is {-12, -2}

Solution:

Given equation is:

`x^2 + 14x = -24`

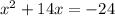
We have to find the solution set of this equation by completing the square

First, rearrange the equation so that only zero will be on the right side:

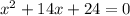`x^2 + 14x + 24 = 0` ----- eqn 1

The general form of quadratic equation is:

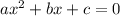`ax^2 + bx + c = 0` where
`a \\eq 0`

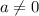
On comparing the given eqn 1 with general quadratic equation, we get

a = 1

b = 14

c = 24

In completing the square, we take half of coefficient of middle term "x" and then square it. Then we add it on both sides of the equation

So to complete the square, add
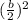`((b)/(2))^2` to both sides of the equation

`x^2 + 14x + 24 + ((14)/(2))^2 = ((14)/(2))^2`

`x^2 + 14x + 24 + 7^2 = 7^2\\\\x^2 + 14x + 24 + 49 = 49`

`x^2 + 14x + 24 + 49 = 49\\\\x^2 + 14x + 49 = 49 - 24\\\\x^2 + 14x + 49 = 25\\\\(x + 7)(x + 7) = 25\\\\(x + 7)^2 = 25`

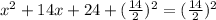
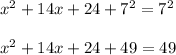
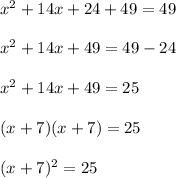
Take square root on both sides

`x + 7 = √(25)`

`x+7=\pm 5`

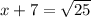
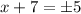
Now make two equations

x + 7 = + 5 and x + 7 = -5

x = +5 - 7 = -2

x = -2

And,

x + 7 = -5

x = -5 - 7 = -12

x = -12

Therefore, the solution set of the equation is {-12, -2} and option A is correct