Question

Beth enlarged the triangle below by a scale of 5. Height 3.5 cm, width 4cm. She found the area of the enlarged triangle. Her work is shown below. 1/2(4)(3.5)(5)= 35 cm2What was beth’s error?

Answer 1

Ben's mistake was not multiplying the area of the original triangle by the scale factor squared.

Explanation:

we know that

The dilation is a non-rigid transformation that produce similar figures

so

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z ----> the scale factor

x ----> the area of the enlarged triangle

y ----> the area of the original triangle

so

`z^(2)=(x)/(y)`

`x=y(z^2)`

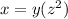
The area of the enlarged triangle is equal to the area of the original triangle multiplied by the scale factor squared

`x=(1)/(2)(4)(3.5)(5^2)=175\ cm^2`

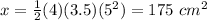
therefore

Ben's mistake was not multiplying the area of the original triangle by the scale factor squared.