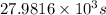Question

The moon Phobos orbits Mars

(mass = 6.42 x 1023 kg) at a distance
of 9.38 x 106 m. What is its period of
orbit?​

Answer 1

27583.78 s

Step-by-step explanation:

Acellus

Answer 2

`27.9816 * 10^(3) s` is the period of orbit.

Explanation:

The equation that is useful in describing satellites motion is Newton form after Kepler's Third Law. The period of the satellite (T) and the average distance to the central body (R) are related as the following equation:

`(T^(2))/(R^(3))=(4 * \pi^(2))/(G * M_(c e n t r a l))`

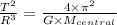
Where,

T is the period of the orbit

R is the average radius of orbit

G is gravitational constant
`6.673 * 10^(-11) \mathrm{N} \cdot \mathrm{m}^(2) / \mathrm{kg}^(2)`

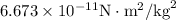
Here, given data

`M=6.23 * 10^(23) \mathrm{kg}`

`R=9.38 * 10^(6) \mathrm{m}`

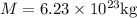
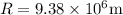
Substitute the given values, we get T as

`(T^(2))/(\left(9.38 * 10^(6)\right)^(3))=(4 *(3.14)^(2))/(\left(6.673 * 10^(-11)\right) * 6.23 * 10^(23))`

`T^(2)=(4 * 9.8596 * 825.29 * 10^(18))/(41.57 * 10^(12))`

`T^(2)=(32548.12 * 10^(18-12))/(41.57)=782.97 * 10^(6)`

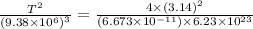
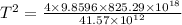
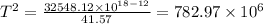
Taking square root, we get

`T=27.9816 * 10^(3) s`