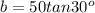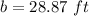Question

A shadow cast by a building is 50 ft long when the angle of inclination of the sun is 30 degrees. How tall is the building?

Answer 1

28.87 ft

Explanation:

Triangles And Trigonometry

In right triangles, some special relationships hold like Pythagoras's theorem and the three basic definitions of trigonometric functions. If a,b,c are the length of the sides of a right triangle, being c its hypotenuse and a and b its legs, then

`c^2=a^2+b^2`

`\displaystyle sin\alpha =(b)/(c)`

`\displaystyle cos\alpha =(a)/(c)`

`\displaystyle tan\alpha =(b)/(a)`

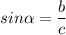
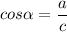
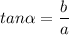
where b is the side opposite to the angle
`\alpha` and a is the side adjacent to the angle
`\alpha`

Please refer to the image below

In our problem, the building is the height of the triangle (b), its shadow is the width (a), and the distance from the tip of the shadow and the top of the building is the hypotenuse (c). We know the angle of inclination is 30°. The known side is one leg of the triangle, and the height of the building is the other leg. The relation to use is

`\displaystyle tan30^o =(b)/(50)`

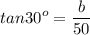
Solving for b

`b=50tan30^o`

`b=28.87\ ft`