Question

Which of the following could be an example of a function with a domain [a,∞) and a range (-∞,b] where a > 0 and b > 0?

A)f(x)= √x+a -b

B) f(x)= -√x-a +b

C)f(x)= 3√x+a -b

D) f(x)= ^3√(x-b) +a

Answer 1

its b

Explanation:

a . p e x

Answer 2

`f(x) = - √(x - a) + b`

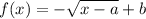
Explanation:

We are given a few functions in options and we have to choose from them that has the domain [a,∞) and range (-∞,b].

Now, for domain i.e. the value of x ≥ a.

Therefore, the value of y must be a function of
`√(x - a)`

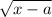
So, there is only one function
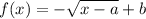`f(x) = - √(x - a) + b` ............ (1), that has the term
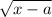`√(x - a)` in it.

Now, for x = a, the value of f(x) becomes b and for x = ∞ the function f(x) value becomes -∞.

Therefore, the range of the function will be (-∞,b] i.e. y ≤ b.

Hence, the required function is
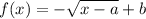`f(x) = - √(x - a) + b`. (Answer)