Function f is an exponential function. It predicts the value of a famous painting, in thousands of dollars, as a function of the number of years since it was last purchased. Wha…

Function f is an exponential function. It predicts the value of a famous painting, in thousands of dollars, as a function of the number of years since it was last purchased. Wha…

asked Sep 11, 2020 205k views

2 Answers

Answer:

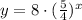
$y=8 \cdot ((5)/(4))^x$

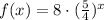
$f(x)=8 \cdot ((5)/(4))^x$

or

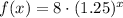
$f(x)=8 \cdot (1.25)^x$

Explanation:

We are going to see if the exponential curve is of the form:

$y=a \cdot b^x$ , (
$b\\eq 0$ ).

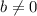If you are given the
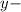intercept, then
is easy to find.

It is just the
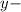coordinate of the
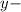intercept is your value for
.

(Why? The
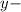intercept happens when
x=0 . Replacing
with 0 gives
$y=a \cdot b^0=a \cdot 1=a$ . This says when
$x=0 \text{ that} y=a$ .)

So
a=8 .

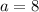So our function so far looks like this:

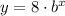
$y=8 \cdot b^x$

Now to find
we need another point. We have two more points. So we will find
using one of them and verify for our resulting equation works for the other.

Let's do this.

We are given
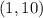(1,10) is a point on our curve.

So when
x=1 ,
y=10 .

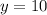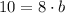
$10=8 \cdot b^1$

$10=8 \cdot b$

Divide both sides by 8:

(10)/(8)=b

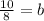
Reduce the fraction:

(5)/(4)=b

So the equation if it works out for the other point given is:

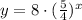
$y=8 \cdot ((5)/(4))^x$

Let's try it. So the last point given that we need to satisfy is
(2,12.5) .

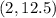This says when
x=2 ,
y=12.5 .

Let's replace
with 2 and see what we get for
:

$y=8 \cdot ((5)/(4))^2$

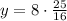
$y=8 \cdot (25)/(16)$

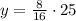
$y=(8)/(16) \cdot 25$

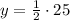
$y=(1)/(2) \cdot 25}$

y=(25)/(2)

y=12.5

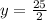
So we are good. We have found an equation satisfying all 3 points given.

The equation is
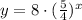$y=8 \cdot ((5)/(4))^x$ .

Configurator answered Sep 15, 2020

by Configurator

7.8k points

← Prev Question Next Question →

Search Qammunity.org