Answer:
The rate of change of radius of the spherical balloon is 0.0282 cm per sec .
Explanation:
Given as :
The rate at which air is filled inside balloon = 7 cm³ per sec
Let The radius = r cm
And The volume of balloon = v = 367 cm³
let The change of radius =
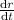
∵ volume = 367 cm³
∵ volume of sphere =
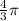 r³
r³
i.e 367 =
 ×
×
 × r³
× r³
or, r³ =
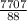
So, r³ = 87.57
∴ r =
![\sqrt[3]{87.57}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/y1w3cfdiqdh9093voy5cxt7l04u6c0m844.png) = 4.44 cm
= 4.44 cm
I.e r = 4.44 cm
Now,
 =
=
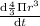
Or,
 = 4
= 4
 r²×
r²×
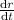
Or, 7 = 4
 (4.44)²×
(4.44)²×
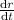
Or, 7 = 4 × 3.14 × 19.71 ×
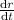
Or, 7 = 247.55 ×
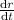
∴
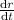 =
=

Or,
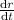 = 0.0282 cm per sec
= 0.0282 cm per sec
Hence, The rate of change of radius of the spherical balloon is 0.0282 cm per sec . Answer